Calcul de la Variance dans Excel : Un Guide avec Exemples
La variance est une mesure statistique qui indique à quel point un ensemble de nombres est dispersé. C'est un concept crucial dans les domaines de la finance, des sciences et bien d'autres, nous aidant à comprendre la variabilité ou la dispersion au sein de nos ensembles de données. Excel offre une méthode simple pour calculer la variance, ce qui la rend accessible aussi bien aux débutants qu'aux utilisateurs avancés. Dans cet article, nous explorerons comment faire cela avec des exemples clairs.
Qu'est-ce que la variance ?
Introduction aux fonctions de variance dans Excel
Comment calculer la variance dans Excel ?
- VAR.S vs VAR.P – Calculer la variance à partir d'un échantillon ou d'une population
- VAR.S vs VARA – Calculer la variance en incluant ou excluant les textes et valeurs logiques
Variance vs Écart-type
Qu'est-ce que la variance ?
La variance est un terme statistique qui décrit dans quelle mesure les nombres d'un ensemble de données diffèrent de la moyenne, ou de l'espérance mathématique, des nombres. Essentiellement, elle mesure à quel point les nombres sont dispersés. Un point clé pour comprendre la variance est de reconnaître qu'elle quantifie le degré de variation ou de dispersion au sein d'un ensemble de valeurs. Une variance élevée indique que les nombres sont dispersés ; une faible variance suggère qu'ils sont regroupés près de la moyenne.
Un exemple simple pour illustrer la variance :
Scénario : Considérons une classe de cinq étudiants et leurs scores à un test de mathématiques sur 100. Les scores sont 90, 92, 88, 91 et 89.
Calculer la Moyenne : D'abord, nous trouvons la moyenne (moyenne) des scores. La moyenne est
Calculer la Variance : Ensuite, nous calculons la variance. Cela implique de soustraire la moyenne de chaque score, d'élever le résultat au carré, puis de faire la moyenne de ces différences au carré.
= [0 + 4 + 4 + 1 + 1] / 5
= 10 / 5
= 2
Un graphique affichant la répartition des scores :
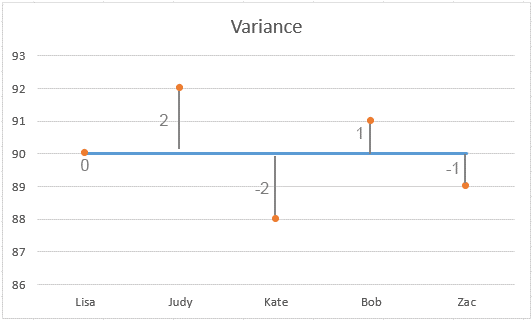
Comprendre le Résultat :
Faible Variance : Dans cet exemple, la variance est de 2. C'est relativement bas, indiquant que la plupart des scores sont proches de la moyenne (90). Plus la variance est faible, plus les nombres individuels de l'ensemble sont proches de la moyenne.
Variance Nulle : Si tous les étudiants avaient obtenu exactement 90, la variance serait de 0, indiquant aucune variabilité. Chaque score serait identique.
Variance Élevée : À l'inverse, une variance plus élevée indiquerait que les scores sont plus dispersés par rapport à la moyenne, montrant une plus grande variabilité dans les performances des étudiants.
En résumé, la variance nous donne une valeur numérique qui aide à quantifier à quel point les scores (ou tout ensemble de nombres) s'écartent de la valeur moyenne, fournissant des informations sur la cohérence ou la variabilité des données.
Introduction aux fonctions de variance dans Excel
Excel propose plusieurs fonctions pour calculer la variance, chacune conçue pour différents scénarios de données.
Comprendre ces fonctions est crucial pour une analyse statistique précise.
VAR.S (Variance d'échantillon, uniquement incluant les nombres) :
- Calcule la variance basée sur un échantillon d'une population.
- Le mieux adapté lors de l'analyse d'un sous-ensemble de données pour en inférer sur l'ensemble.
VAR.P (Variance de population, uniquement incluant les nombres) :
- Calcule la variance pour toute la population.
- Idéal lorsque vous avez des données complètes et non seulement un échantillon.
VARA (Variance d'échantillon, incluant texte et valeurs logiques) :
- Similaire à VAR.S mais inclut du texte et des valeurs logiques dans le calcul (le texte est traité comme 0, VRAI comme 1, FAUX comme 0).
- Utile lorsque votre ensemble de données contient des types mixtes (nombres, texte et valeurs logiques).
VARPA (Variance de population, incluant texte et valeurs logiques) :
- La version de variance de population de VARA.
- Inclut tous les types de données dans le calcul de la variance pour toute la population.
VAR (Variance d'échantillon héritée) :
- Une ancienne version de VAR.S, principalement utilisée dans Excel 2007 et versions antérieures.
- Il est recommandé d'utiliser VAR.S dans les versions plus récentes pour assurer cohérence et clarté.
VARP (Variance de population héritée) :
- L'ancienne version de VAR.P.
- Comme VAR, il est recommandé d'utiliser VAR.P dans les versions plus récentes d'Excel.
Différences et Comparaisons :
- Échantillon vs Population : VAR.S et VARA sont pour les échantillons, tandis que VAR.P et VARPA sont pour toute la population.
- Considération du Type de Données : VARA et VARPA incluent du texte et des valeurs logiques dans le calcul, contrairement à VAR.S et VAR.P.
- Fonctions Héritées vs Modernes : VAR et VARP sont des fonctions anciennes et peuvent être remplacées par VAR.S et VAR.P pour une meilleure compatibilité avec les versions actuelles d'Excel.
Tableau de Comparaison :
| Fonction | Type de Données Pris en Compte | Population ou Échantillon | Cas d'Utilisation |
| VAR.S | Uniquement Nombres | Échantillon | Variance d'échantillon pour les données numériques |
| VAR.P | Uniquement Nombres | Population | Variance de population pour les nombres |
| VARA | Nombres, Texte, Valeurs Logiques | Échantillon | Variance d'échantillon pour les données mixtes |
| VARPA | Nombres, Texte, Valeurs Logiques | Population | Variance de population pour les données mixtes |
| VAR | Uniquement Nombres | Échantillon | Fonction héritée pour la variance d'échantillon |
| VARP | Uniquement Nombres | Population | Fonction héritée pour la variance de population |

Découvrez la magie d'Excel avec Kutools AI
- Exécution intelligente : Effectuez des opérations sur les cellules, analysez les données et créez des graphiques, le tout piloté par des commandes simples.
- Formules personnalisées : Générez des formules adaptées pour rationaliser vos flux de travail.
- Codage VBA : Écrivez et implémentez du code VBA sans effort.
- Interprétation des formules : Comprenez facilement des formules complexes.
- Traduction de texte : Surmontez les barrières linguistiques dans vos feuilles de calcul.
Comment calculer la variance dans Excel ?
Dans cette section, nous fournirons deux exemples pour démontrer comment calculer la variance dans Excel et expliquer les différences entre les différentes fonctions de variance. Par conséquent, vous verrez que différentes fonctions de variance donnent des résultats entièrement différents pour les mêmes données d'exemple.
VAR.S vs VAR.P – Calculer la variance à partir d'un échantillon ou d'une population
Scénario : Calcul de la variance pour un petit échantillon d'une population par rapport à la population entière.
Exemple : Calculez la variance pour les valeurs dans la colonne A2:A12.
Formule : Sélectionnez une cellule vide et tapez une des formules ci-dessous selon vos besoins, puis appuyez sur Entrée.
Obtenir les variances pour un échantillon d'un grand jeu de données (en supposant que les valeurs dans A2:A12 font partie d'un grand jeu de données)
=VAR.S(A2:A12)
Obtenir la variance pour toute la population (en supposant que les valeurs dans A2:A12 représentent l'ensemble du jeu de données)
=VAR.P(A2:A12)
Comme vous pouvez le voir, les mêmes valeurs mais l'utilisation de différentes fonctions de variance donneront des résultats différents.
Pourquoi les résultats de VAR.S et VAR.P sont-ils différents ?
- VAR.S : Cette fonction est utilisée lorsque votre jeu de données représente un échantillon d'une population plus large. Elle calcule la variance basée sur la méthode « n-1 », où « n » est le nombre de points de données dans l'échantillon. L'utilisation de « n-1 » au lieu de « n » comme dénominateur corrige le biais dans l'échantillon, en faisant un estimateur sans biais de la variance de la population. Elle fournit une estimation de la façon dont les données de l'échantillon varient autour de la moyenne de l'échantillon.
- VAR.P : Cette fonction est utilisée lorsque votre jeu de données représente une population entière, et non seulement un échantillon. Elle calcule la variance basée sur la méthode « n », où « n » est le nombre de points de données dans la population. Elle suppose que le jeu de données couvre toute la population, donc il n'est pas nécessaire de corriger le biais comme dans VAR.S.
- En résumé, la différence clé réside dans le dénominateur de la formule. VAR.S utilise « n-1 » pour tenir compte de la nature échantillonnée des données, tandis que VAR.P utilise « n » pour les données de population où aucun échantillonnage n'est impliqué. Selon votre jeu de données et si c'est un échantillon ou une population complète, vous devriez choisir la fonction appropriée pour calculer la variance.
VAR.S vs VARA – Calculer la variance en incluant ou excluant les textes et valeurs logiques
Scénario : Décider d'inclure ou non les valeurs logiques et les textes dans le calcul de la variance.
Exemple : Calculez la variance pour les valeurs dans la colonne A2:A12.
Formule : Sélectionnez une cellule vide et tapez une des formules ci-dessous selon vos besoins, puis appuyez sur Entrée.
Obtenir les variances pour un échantillon d'un grand jeu de données en ignorant les textes et les valeurs logiques.
=VAR.S(A2:A12)
Obtenir la variance pour un échantillon d'un grand jeu de données en incluant les textes et les valeurs logiques.
=VARA(A2:A12)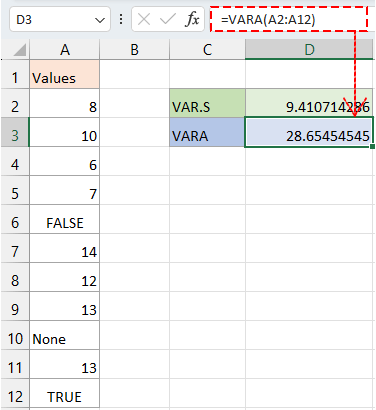
Rendre les Calculs de Date et Heure Faciles
Kutools for Excel's Date Time Helper est un outil incroyablement efficace conçu pour simplifier les calculs complexes de date et heure. Essayez-le et voyez comment il transforme votre expérience de gestion des données !
Variance vs Écart-type
Similarités :
Mesure de Dispersion :
La variance et l'écart-type sont tous deux des mesures statistiques utilisées pour décrire la dispersion ou la variabilité au sein d'un ensemble de données. Ils quantifient à quel point les nombres individuels de l'ensemble s'écartent de la moyenne (moyenne).
Analyse de Données :
Les deux sont couramment utilisés dans l'analyse statistique pour comprendre la variabilité des données. Ils sont essentiels dans des domaines tels que la finance, la recherche, le contrôle qualité, et plus encore.
Calculé à partir de la Moyenne :
Le calcul de la variance et de l'écart-type commence par la moyenne de l'ensemble de données. Ils évaluent la variabilité par rapport à cette valeur centrale.
Différences :
Unités de Mesure :
Variance : Unités au carré des données originales. Par exemple, si les données sont en mètres, la variance sera en mètres carrés.
Écart-type : Mêmes unités que les données originales. Pour continuer l'exemple, si les données sont en mètres, l'écart-type sera également en mètres.
Interprétation :
Variance : Fournit une estimation au carré qui peut être moins intuitive à interpréter car elle n'est pas à la même échelle que les données originales.
Écart-type : Plus facile à interpréter car il est dans les mêmes unités que les données. Il indique la distance moyenne des points de données par rapport à la moyenne.
Définition Mathématique :
Variance : La moyenne des différences au carré par rapport à la Moyenne.
Écart-type : La racine carrée de la variance.
Sensibilité aux Valeurs Extrêmes :
Variance : Plus sensible aux valeurs aberrantes car elle met les différences au carré.
Écart-type : Bien qu'affecté par les valeurs aberrantes, il est moins sensible par rapport à la variance en raison de la racine carrée.
Applications :
Variance :
Utilisée lorsque l'accent est mis sur l'amplitude de la dispersion au carré.
Bénéfique dans les modèles statistiques et les calculs où la mise au carré est nécessaire pour annuler les valeurs négatives.
Souvent utilisée dans les modèles financiers pour l'évaluation des risques, car elle mesure la volatilité.
Écart-type :
Plus couramment utilisé dans les rapports et applications quotidiennes en raison de sa relation directe avec l'échelle des données.
Essentiel dans la recherche empirique pour comprendre la variabilité.
Fréquemment utilisé dans le contrôle qualité, les bulletins météo et les scores standardisés dans les tests.
Conclusion :
Bien que la variance et l'écart-type servent tous deux à mesurer la dispersion d'un ensemble de données, leurs applications diffèrent en raison de leur unité de mesure et de leur interprétation. L'écart-type, avec sa relation directe à l'échelle des données, tend à être plus convivial, en particulier dans des contextes pratiques et quotidiens. La variance, en revanche, est souvent mieux adaptée aux modèles mathématiques et statistiques.
Cette vue d'ensemble et cette comparaison devraient fournir une compréhension claire de quand et pourquoi utiliser chaque fonction de variance dans Excel, permettant une analyse de données plus précise et significative. Pour plus de stratégies révolutionnaires dans Excel qui peuvent améliorer votre gestion des données, explorez davantage ici..
Les meilleurs outils de productivité pour Office
Kutools pour Excel - Vous aide à vous démarquer de la foule
Kutools pour Excel compte plus de 300 fonctionnalités, garantissant que ce dont vous avez besoin est à portée d'un clic...
Office Tab - Activer la lecture et l'édition par onglets dans Microsoft Office (y compris Excel)
- Une seconde pour passer entre des dizaines de documents ouverts !
- Réduit de centaines le nombre de clics souris pour vous chaque jour, dites adieu à la main de la souris.
- Augmente votre productivité de 50 % lors de la visualisation et de l'édition de plusieurs documents.
- Apporte des onglets efficaces à Office (y compris Excel), tout comme Chrome, Edge et Firefox.
Table des matières
- Qu'est-ce que la variance ?
- Introduction aux fonctions de variance dans Excel
- Comment calculer la variance dans Excel ?
- VAR.S vs VAR.P – Calculer la variance à partir d'un échantillon ou d'une population
- VAR.S vs VARA – Calculer la variance en incluant ou excluant les textes et valeurs logiques
- Variance vs Écart-type
- Articles Connexes
- Meilleurs Outils de Productivité pour Office
- Commentaires